Le Tetra Master est le jeu de cartes facultatif du jeu Final Fantasy 9. Son fonctionnement est, en surface, similaire au Triple Triad — le jeu de cartes de Final Fantasy 8 — cependant, même s'il est possible de capturer une intuition générale nous permettant de gagner, pour peu que l'on possède des bonnes cartes, après plus d'une centaine de parties, je dois avouer avoir accepté le fait que, juste en jouant au jeu, et en lisant tous les didacticiels en jeu, je fusse incapable d'en comprendre l'ensemble des règles, me poussant à me documenter pour comprendre ce que j'avais raté. L'absence d' aucune règle dans le jeu (ou le manuel) m'a exaspéré, me poussant à écrire cet article ...
L'enfer du Tetra Master
Attention, ma critique salée ne porte que sur le jeu Tetra Master. Bien que je puisse parfaitement comprendre (et accepter) certaines critiques formulées à l'égard du neuvième opus de la saga, j'ai, peut-être par nostalgie, beaucoup apprécié le jeu. De plus, le jeu de cartes n'est pas un élément bloquant pour le progrès dans l'aventure, il est donc possible de parfaitement apprécier le jeu, tout en ne conservant qu'une très légère frustration de ne pas comprendre les rouages complexes — et discutablement inférables — de son système de règles.
Certaines personnes trouveront ça très étrange de revenir sur ce jeu, plus de 22 ans après sa sortie en Europe... c'est vrai ! Je dois vous avouer que je trouve ça très rigolo de tâcher de transformer ce site web en un genre de bibliothèque poussiéreuse, remplie de savoirs inutiles.
Mise en contexte
J'ai découvert la saga Final Fantasy par le biais du 7ème opus, à la fin des années 90, regardant avidement mon cousin, Thomas, y jouer. J'avais été très marqué, et je suis devenu un grand amateur de la série, pour ses ambiances, ses musiques, et ses histoires. Par contre, étant très jeune, et n'ayant pour seule expérience du genre JRPG Pokemon rouge, je me souciais peu de mécaniques — quelle horreur, me direz-vous, je passais à côté de ce qui fait qu'un jeu vidéo est un jeu — et donc je lisais peu les didacticiels de jeu, ne cherchant qu'à progresser dans l'histoire.
Même si la série Final Fantasy — du moins, les épisodes parvenus jusqu'en Europe à cette époque — n'est pas réputée pour être une collection de jeux difficile, ne pas s'embarrasser de la compréhension, par exemple, du sysème de materia, dans Final Fantasy 7 peut rendre la progression de l'aventure très complexe. Et oui, bien que les opus 6, 7, 8 et 9 de Final Fantasy soient, en terme de Skill Ceiling, similaires aux versions rouge et bleue de Pokemon, j'ai l'intuition que le Skill Floor des trois Final Fantasy est largement plus élevé.
Gardant une sympathie, pendant plusieurs années, sur ces jeux que je n'avais jamais terminés, des années plus tard, je décidais d'y rejouer, avec l'ambition de les terminer. De plus, à cette époque, mon intérêt en tant que programmeur se portait sur la série RPGMaker (un logiciel jouet pour construire des RPGs, en offrant une interface de de programmation pour la construction de systèmes originaux et laissant un très grande liberté de personnalisation pour les utilisateurs plus chevronnés), jouer à des classiques du genre me semblait être une très bonne approche !
Comme les JRPGs sont, très souvent, des jeux longs, et que je n'y jouais pas à la fréquence d'un hardcore gamer, presque 10 ans plus tard, après avoir terminé FF6, FF7 et FF8, mon bilan était clair: lire les didacticiels et comprendre les différentes mécaniques de jeu rend l'expérience de jeu largement plus facile. Même s'il existe des subtilités dans chacun de ces opus, relevant plus du Skill Ceiling, les jeux étaient globalement très simples — ce qui n'est pas une critique — et je pouvais attaquer FF9, sereinement.
Simple, mais pas sur tous les aspects
Comme ses prédécesseurs, Final Fantasy 9 n'est pas un jeu compliqué. Les mécaniques de jeu sont faciles d'accès et, même si parfois les combats peuvent manquer de rythme — et le mécanisme de transe peut être frustrant quand on vient des deux précédents jeux — on comprend rapidement comment être efficace. La source de ma frustration provient du jeu de cartes. Comme son prédécesseur, le jeu embarque un système ad-hoc, le Tetra Master, un jeu de cartes est introduit assez rapidement dans sa diégèse. En tant que joueur, je suis généralement assez favorable à la diversification (et la prolifération) de systèmes ad-hoc, surtout dans les JRPGs, qui bénéficient, généralement, d'une assez longue durée de vie et qui, du moins, à cette époque, étaient souvent linéaires parce qu'ils permettent parfois de changer le rythme et d'introduire des quêtes annexes amusantes. Dans le jeu, le Tetra Master est introduit comme un jeu de cartes simple, et il est très rapidement possible de récupérer ses premières cartes et d'apprendre les pretendues règles du jeu.
Après plus d'une centaine de parties et, tout en ayant lu consciencieusement les différents fragments de règles éparpillées dans le jeu — notamment via les conseils de Jack — j'en suis arrivé à la conclusion suivante : je n'étais jamais serein lors d'une partie, car même si j'avais capturé l'idée générale du jeu, il semblait me manquer quelque chose dans la compréhension des règles.
Découverte des règles via Internet
Frustré que, malgŕe mon expérience dans le jeu, je semblais passer à coté de plusieurs subtilités, je fis ce que, à l'époque (aux alentours de 2000), je ne pouvais pas faire, j'ai cherché sur le net. J'ai été amusé de voir qu'en 2023, il existe toujours des sites, à l'apparence des sites du début des années 2000 qui forment une base de connaissances impressionnantes sur la licence sur lesquels j'ai pu trouvé des règles détaillées du Tetra Master et, en effet, il me manquait beaucoup d'éléments pour comprendre l'ensemble des règles du jeu. D'ailleurs, durant mes recherches, j'ai eu l'occasion de trouver un grand nombre de messages publiés sur des forums de joueurs tout aussi désabusés que moi. Une fois les règles découvertes, une autre question s'est naturellement posée : "Comment ces sites ont-ils découvert ces règles ?".
Mon premier réflexe a été de consulter le manuel
d'origine
qui, possède une section dédiée au Tetra Master (page 22 et 23).
Malheureusement, elle ne donne pas plus d'informations que ce que l'on
apprend dans le jeu. Cependant, l'encart Card Ability Points de la
page 22 :
Every card has a set of numbers and letters that represents the strength of the card, which comes into play during card battles. Generally, the higher the number, the stronger the card. Try to figure out the effects of numbers and letters on each card.
Sapristi, le manuel nous provoque ! En cherchant plus profondément, j'ai trouvé un sombre document, publié en Novembre 2000, et mis à jour jusqu'en Juin 2001, qui semble être la base du savoir collectif des règles du jeu. Fruit d'une investigation poussée — incluant des demandes à Squaresoft et probablement un peu de reverse-engineering — Le document a été initié en vue d'établir un ensemble de règles exhaustives du jeu pour être porté en jeu de plateau et semble avoir été l'aboutissement d'une très jolie collaboration.
Un autre point très amusant du document, au-delà d'expliquer les règles, est qu'il met en lumière une citation extraordinaire d'un certain Drew Cosner, membre de l'équipe de rédaction de feu The Gaming Intelligence Agency, un site éteint en 2015 proposant des revues de jeux vidéo.
Anyway, here it is: how the hell are you supposed to play Tetra Masters in FFIX? As far as I can tell, you place your cards on the board at random and your opponent randomly puts his cards down causing random cards to flip over at random, leading to the random card battle which is apparently won completely at random. In the end, one of you wins. At random.
Démontrant que non, je n'étais pas le seul ayant été frappé d'incompréhension par des règles, je ne me contente que de m'inscrire, 20 ans plus tard, dans la collectivité des joueurs désabusés par cet étrange jeu de cartes, pourtant tant apprécié des habitants de l'univers imaginaire dans lequel se déroule l'histoire de, malgré tout, l'excellent Final Fantasy 9.
Le Tetra Master
Comme je l'ai évoqué dans cette très longue introduction, il existe, depuis la publication du "sombre document", énormément de ressources en ligne pour apprendre les règles de l'infernal Tetra Master. Alors à quoi bon décider, en 2023, d'en écrire une nouvelle ? Même si l'article a essentiellement pour objectif de râler sur la complexité des règles et sur leur non-découvrabilité, je pense que documenter l'ensemble des règles, à ma manière — mais en me basant sur le document précédemment cité — appuiera mes propos, et me permet, un peu gratuitement, d'ajouter du contenu à mon site.
Les cartes dans l'histoire
Les cartes sont très rapidement introduites dans le lore du jeu. En effet, elles semblent susciter, dès les premiers instants de jeux, un intérêt tout particulier pour Bibi. D'ailleurs, lors de la fête de la chasse, il réclamme pour récompense la carte Aérothéatre, une carte largement superieure au niveau des cartes acquises à ce stade de l'aventure. Bien que les cartes ne changent absolument pas la progression dans l'histoire et ne procurent aucun bonus, on apprend que beaucoup des habitants de l'univers du jeu jouent à ces cartes et il existe même un tournoi de cartes (que vous pouvez perdre sans crainte).
Si ces cartes n'apportent pas de bonus additionnel, elles permettent de satisfaire la collectionnite aigüe de certains joueurs et, comme beaucoup de systèmes de jeux ad-hoc dans le JRPGs, les parties de cartes permettent de légèrement rompre la linéarité du jeu, construisant un réseau de petites quêtes annexes se greffant à la trame principale ou à d'autres quêtes et systèmes annexes.
En bref, si les règles du jeu avait été inférables... son intégration aurait été, selon moi, une excellente idée (un peu à la manière du Triple Triad de FF8), malheureusement, comme nous allons le voir... ce n'est absolument pas le cas !
La collecte des cartes
Les cartes faisant partie de la diégèse du jeu, il est normal qu'il existe plusieurs moyens d'en collecter. Après avoir évoqué les différentes méthodes pour collecter de nouvelles cartes, je tâcherai de, subjectivement, définir l'approche la plus efficace :
-
Les recevoir de personnages
C'est la première approche auquel nous sommes confrontés. En effet, dès le début de l'aventure, Bibi aura l'occasion de collecter des cartes et de se voir enseigner les bases du jeu (oui, juste les bases, soit absolument trop peu d'information pour comprendre les règles. Fichus PNJs, incapables de nous donner des informations exhaustives). -
Les trouver
Comme dans tout JRPG qui se respecte, les donjons et les villages regorgent de trésors, dans FF9, en plus des coffres, il est possible de trouver des objets cachés — les frôler fera apparaitre un phylactère habité d'un point d'exclamation. Parfois, vous découvrirez des cartes. A noter qu'elles peuvent aussi faire partie des trésors découvrables au moyen de Chocographes. -
En récompense de combats
Il arrive parfois que certains adversaires offrent en récompense une ou plusieurs cartes. Très souvent, la carte reçue correspondra à l'un des monstres présent dans le combat — logique, pour une fois. -
Les acheter
Il est possible d'acheter, pour100 gilsdes cartes dans la ville de Treno. Le prix étant très bas, les cartes disponibles à la vente seront, de facto relativement peu intéressantes. -
Les gagner
Nous le détaillerons plus tard en expliquant les règles mais gagner des parties de cartes permet de prendre une ou cinq cartes, en cas de victoire, à son adversaire. Comme certains PNJs sont des joueurs expérimentés — notamment au tournois de cartes de Treno — il est possible de collecter des cartes puissantes dès que l'on atteint un certain niveau de progression dans le jeu.
Naïvement, en observant cette liste, on pourrait rapidement arriver à la conclusion que la manière la plus efficace de gagner un maximum de cartes est de défier le plus d'adversaires possible. Cependant, et c'est la raison d'être de cet article, le jeu étant très compliqué, j'ai l'intime conviction que pour se construire un deck efficace, il vaut mieux combattre le plus de monstres possibles. En effet, les monstres, lors des rencontres aléatoires, ont une probabilité de laisser une carte en récompense. En plus de la carte, combattre des monstres fait gagner de l'expérience et d'autres objets, donnant donc, à la collecte de carte, une utilité concrète à la progression dans l'aventure. Cependant, défier des adversaires est aussi nécessaire, comme nous le verrons dans l'exposition du détail des règles.
Une brève note sur l'aléatoire
Chaque carte est dotée de plusieurs caractéristiques permettant d'estimer sa force. Donc deux cartes de mêmes illustrations peuvent être différentes. Un point simultanément amusant et frustrant est que ces caractéristiques ne sont pas définies tant que l'on ne possède pas la carte. En d'autres mots, les cartes données par d'autres personnages, ou trouvées dans les villages et les donjons, fixent leurs caractéristiques une fois trouvées. Il est donc possible, et recommandé, de sauvegarder avant de collecter une carte et de relancer le jeu tant que l'on est pas satisfait des caractéristiques de la carte. Et cette astuce fonctionne pour toutes les cartes, incluant les cartes rares.
Tout au long de ce guide, je me plaindrai assez régulièrement sur l'aléatoire qui amplifie le non-déterminisme du jeu. La variabilité des statistiques d'une carte trouvée ou reçue en est le premier témoignage.
Les règles selon le manuel
Comme évoqué dans la mise en contexte de cet article, le manuel d'origine dédie deux pages au Tetra Master. Globalement, les informations proposées par le manuel ne sont pas beaucoup plus fournies que celle que l'on peut collecter pendant le jeu, cependant, pour que vous compreniez ma frustation, je vais le paraphraser, ce qui rendra l'explication détaillée suivant cette rubrique encore plus impresionnante !
Défier un adversaire
C'est probablement la partie la plus exhaustive du guide, en effet, certains PNJs jouent aux cartes. Pour les défier, il suffit de s'approcher d'eux et d'interagir avec la touche carré.
Règles basiques
Cette partie décrit dans les très grandes lignes le déroulé du jeu, en ommettant beaucoup de détails :
Vous et votre opposant placez alternativement 5 cartes sur une grille de 4x4 cases. Il est possible de gagner les cartes de l'adversaire en fonction de où une carte est placée. Une fois que toutes les cartes sont placées, le joueur qui possède le plus de cartes est le gagnant.
De cette section, on comprend que le but est de prendre le plus de cartes à l'adversaire. S'en suivent les différentes méthodes de prise de cartes.
Gagner une carte
Dans les différents schémas, les cartes noires indiquent les cartes du joueur et les grises les cartes de l'opposant. La carte qui est marquée d'un cercle est celle qui vient d'être placée et la flèche entre des motifs de cartes indique la conséquence d'un placement.
"Vous gagnez la carte de l'adversaire quand une flèche de votre carte pointe vers la carte de l'adversaire".
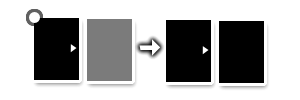
De cette première information (très incomplète), on peut déduire plusieurs choses :
- les cartes ont des flèches — comme la carte de l'adversaire, dans l'exemple, n'en a pas, on peut supposer qu'elles possèdent un nombre variable de flèches, dans des directions variées ;
- on peut supposer que les cartes doivent être adjacentes pour être gagnées ;
- une carte gagnée reste à sa place mais change de couleur pour prendre la couleur de celui qui l'a gagnée.
"Si une flèche de votre carte fait face à une flèche de la carte de l'opposant, il y a bataille, les nombres qui apparaissent sur les cartes se soustrayent et la carte qui a le plus grand nombre gagne l'autre"
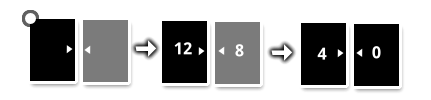
La mécanique de bataille associée au schéma nous apprend de nouveaux éléments sur le déroulé du jeu :
- les cartes possèdent des statistiques ;
- on confirme l'intuition que les flèches présentent sur les cartes varient.
"Quand on gagne une bataille, toutes les cartes ciblées par les flèches de la carte fraîchement gagnée sont aussi gagnées."

La principale idée soulevée par ce schéma est que, en plus des flèches, il est possible de construire une chaîne de prise, un combo qui propage la réussite pour toutes les flèches adjacentes. Cette section soulève plus de questions que d'affirmations :
- les combos se propagent-ils récursivement ? (cette question peut s'adresser rapidement en jouant quelques parties)
- si une carte gagnée dans — le contexte d'un combo se trouve en situation de bataille — est-ce que la bataille a lieu ?
Comme évoqué dans l'introduction, le manuel décrit les cartes comme étant dotées de statistiques — et on a pu le constater dans la situation de bataille — par contre, le manuel est explicite sur le fait qu'il n'expliquera pas comment déchiffrer les statistiques d'une carte et nous verrons que c'est loin d'être si trivial sans aide.
Récompenses et pénalités
En fin de partie, le gagnant peut choisir une carte, parmi les cartes qu'il a réussi à gagner de son adversaire. Par contre, si le gagnant a réussi à gagner toutes les cartes de son adversaire, soit qu'il a joué un Perfect Game, le gagnant prend toutes les cartes de son adversaire, ce qui est une sacré aubaine en cas de victoire, mais peut être incroyablement pénalisant en cas de défaite.
On apprend aussi qu'il est possible de regagner des cartes perdues en rejouant contre les PNJs nous ayant battu.
Nombre limite de cartes et menu
Un petit encart nous apprend que l'on ne peut pas posséder plus de 100 cartes et qu'il est possible de se débarasser de cartes depuis le menu des cartes. C'est un choix étrange car, comme nous l'apprend le menu des cartes, il existe 100 cartes différentes. On peut donc supposer que lorsque l'on est avancé dans la collection de cartes, construire une stratégie exploitant plusieurs même cartes est compromis. D'ailleurs, le fait de consulter ce menu anticipe la frustration que l'on ressentira lors de nos premières parties, en effet, il affiche des informations que l'on ne peut pas relier à ce que l'on a appris en lisant le manuel.
Conclusion de la lecture du manuel
Même s'il reste des parts d'ombres, on pourrait croire que l'on a capturé la logique générale du jeu et que ces parts d'ombres disparaitront en pratiquant le jeu. Je vous rassure tout de suite, ce n'est absolument pas le cas. En effet, bien que le manuel présente quelques stratégies — assez facilement découvrables par soi-même, et donc que je n'introduis pas dans cette section — il semble volontairement laisser une collection d'inconnues, que nous devrions découvrir en jeu, mais, si vous êtes comme moi, vous verrez que les aléas combinés peu d'informations, notamment sur les statistiques des cartes, rendent cette découverte fastidieuse — pour ne pas dire impossible — faisant du Tetra Master, le sujet de multiples railleries. Heureusement, grâce à Internet et à la patience de certains, les règles sont maintenant connues et dans les rubriques qui suivent, je vais essayer d'en donner une description claire ! Les deux seuls points sur lesquels je ne reviendrai pas seront l'utilisation du carré pour démarrer une partie et les récompenses, essentiellement parce que ces deux points sont probablemment les seuls décrits exhaustivement dans le manuel (encore heureux).
Sans plus attendre, passons à une description méticuleuse des règles du Tetra Master. Vous allez voir, vous n'êtes pas à la fin de vos surprises.
Règles détaillées
Décrire méticuleusement et exhaustivement les règles du Tetra Master n'est pas une mince affaire car il est, de mon point de vue, très difficile de définir l'ordre de priorité des informations. La lecture du manuel et la découverte du jeu dans le jeu donnent une idée générale de comment jouer, que l'on pourrait simplement résumer par : "gagner le plus de cartes opposantes possible". Par contre, énumérer toutes les subtilités du jeu semble être un véritable défi. Même si l'on peut accepter d'un jeu que ses rouages soient complexes, on voudrait avoir l'occasion de découvrir, par l'expérimentation, ou la documentation, l'ensemble des règles. Par exemple, les échecs, pour lequel il est facile de résumer l'objectif d'une partie : "mettre le roi dans une situation dans laquelle il peut être pris et où qu'il aille, il reste en situation de prise potentielle", décrire les mouvement de chacune des pièces, les mécaniques de prises, les règles ad-hoc, comme le roc etc, n'est pas une mince affaire, par contre, quand les échecs ont été popularisés, ils étaient adossés à une explication exhaustive des règles. Dans le cas du Tetra Master, il faudra du reverse engineering et de l'investigation !
Initiation d'une partie
Comme le jeu se joue à deux, où chaque joueur démarre avec cinq cartes, les deux prérequis sont :
- posséder 5 cartes (minimum) ;
- trouver un adversaire.
Une fois ces conditions validées, démarrer un combat implique d'interagir avec un personnage en utilisant, par défaut, la touche carré. Il vous sera demandé de choisir les cinq cartes que vous désirez utiliser. On pourrait arguer qu'il faut idéalement prendre ses cinq meilleures cartes, cependant, comme il est possible de perdre soit une, soit cinq cartes, il faut aussi pondérer le risque et la récompense (car comme nous le verrons plus tard, les combos peuvent inverser la vapeur).
Quand une partie commence, une pièce est lancée pour savoir qui est le premier à placer une carte, le joueur a une chance sur deux de commencer. Ensuite chaque joueur place successivement une carte.
Plateau de jeu
Le plateau de jeu est une grille de 4x4, il y a donc 16 cases. Pour
ajouter de la variété le démarrage d'un combat peut générer,
aléatoirement (une fois de plus) entre 0 et 6 cases qui seront
bloquées (sur lesquelles nous ne pourront pas jouer de cartes). Comme
on ne peut retirer que, au maximum, 6 espaces, il y aura toujours,
logiquement assez d'espace pour jouer toutes les cartes.
Voici trois exemples de plateaux pouvant être générés. Le premier n'a
généré aucun obstacle, le second en a généré 3 et le dernier en a
généré 6.
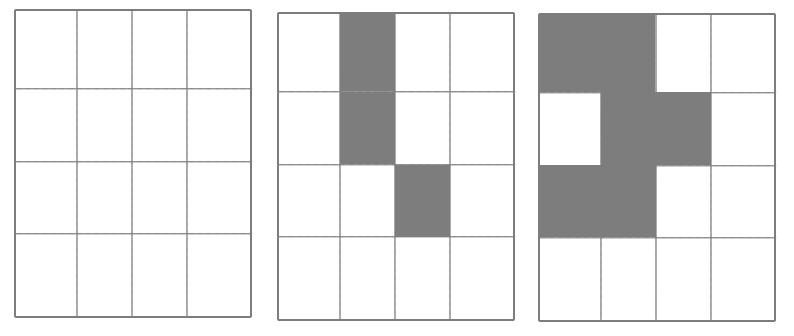
Même si, en introduction de cet article, j'ai un peu râlé sur l'excès d'aléatoire, ici, je trouve que les légères variations de terrains sont une très bonne idée et qu'elles permettent d'échaffauder des stratégies complémentaires. Par exemple dans le troisième exemple, l'emplacement isolé, sans aucune case libre adjacente, permet de placer une carte plus faible, qui ne sera jamais prenable, bloquant ainsi la défaite parfaite et garantissant, dans le pire des cas, la perte d'une seule carte.
Prise de cartes simple
Nous avions vu dans le manuel que pour prendre une carte, il suffit qu'une carte soit placée et toutes les cartes pointées par ses flèches seront gagnées. Dans cet exemple, la carte noire gagne trois cartes ciblées.
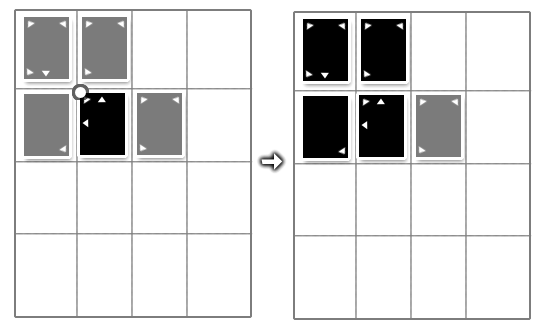
En revanche, pour que les flèches soient effectives, il faut que la carte vienne d'être placée. Dans ce schéma, la carte grise n'affecte pas la carte noire, qui vient d'être jouée :

Parce qu'une carte jouée est offensive et une fois qu'elle a été placée, elle passe en mode défensif. Pour qu'une carte déjà placée en gagne une autre il faut une situation de bataille et/ou de combo, que nous détaillerons dans les sections suivantes.
Bataille
A ce stade de la lecture de l'article, vous devriez vous dire que j'ai largement exagéré la complexité du jeu et que, même si les informations du manuel n'étaient pas complètes, quelques parties devraient suffire à comprendre l'ensemble des mécaniques de jeu ! Rassurez-vous, dans cette section, nous allons rapidement comprendre pourquoi, en jouant au Tetra Master, sans comprendre certaines informations liées aux statistiques des cartes — que l'on peut observer dans une situation de bataille — on est sans arrêt écrasé par une anxiété latente, ne comprenant pas toujours pourquoi est-ce que l'on gagne... ou pire, pourquoi l'on perd.
Pour rappel, quand on place une carte adjacente à une autre carte de couleur différente, on se retrouve face à plusieurs cas de figures :
- la carte placée pointe une ou plusieurs autres cartes adverses, sans opposition de flèches, elle gagne toutes les cartes ciblées ;
- la carte placée ne pointe pas d'autres cartes, et même si elle est pointée par une flèche d'une carte déjà positionnée, aucune carte n'est gagnée ;
- la carte placée pointe une ou plusieurs autres cartes adverses, on entre en situation de bataille et la carte placée est offensive et la carte ciblée est défensive.

Nous avions aussi lu, qu'en situation de bataille, c'est la carte avec le plus grand nombre qui gagne. Et ce qui est génial... c'est que avant de lire les règles, et le document obscur et quelques de tentatives de reverse engineering, j'étais absolument incapable de comprendre comment ce nombre était défini. Accrochez-vous bien, je pense que c'est à partir de ce moment que les concepteurs du Tetra Master — et aussi les gens qui ont validé le Game Design Document — sont devenus fous parce que de mon point de vue, même en jouant des milliers de parties, il est impossible de comprendre comment est défini ce nombre.
Batailles multiples
Bien que nous n'ayons pas encore décrit réellement l'anatomie d'une carte, nous avons spéculé qu'une carte pouvait avoir un nombre multiple de flèches, pointant potentiellement plusieurs cartes différentes. Par exemple dans cette situation :
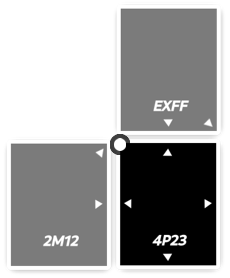
Dans cette situation, on peut voir que la carte jouée est en situation de bataille avec les deux cartes. Alors que généralement, le jeu décide de choisir l'aléatoire ou applique une règle discutablement explicite, pour définir l'ordre de bataille, le joueur offensif décide la carte qu'il désire attaquer en premier. Ce qui permet de mettre en place de véritables stratégies, comme nous le détaillerons lorsque nous expliquerons les combos.
Anatomie d'une carte
Une carte — qui est généralement plus visuelle et jolie que mes
éléments de schémas très sobres — peut avoir un nombre de flèches
directionnelles compris entre 0 et 8, représentant chacune une
direction d'attaque — et, comme on l'a vu dans les batailles, de
défense. On pourrait trouver ça étrange d'avoir (et d'utiliser) des
cartes n'ayant pas de flèches, car elle serait absolument
inefficaces — ne pouvant n'être que prise, et ne pouvant jamais
prendre. Cependant, ces dernières peuvent être redoutablement utiles
pour casser des combos ou, en cas de dernier coup, pour n'assurer
que l'augmentation de 1, en votre faveur, dans le compte des cartes
gagnées.
Ensuite, chaque carte possède un genre d'identifiant cryptique,
difficile à déchiffrer — surtout sur un poste de télévision
cathodique. Par exemple, voici le schéma d'une carte pouvant attaquer
dans toutes les directions, avec comme identifiant : 1P23 :

Nous avons, je le pense, relativement bien compris la mécanique des flèches, et leur rôle, on peut donc spéculer sur le fait que l'identifiant sert à décrire les statistiques d'une carte, et permettent de calculer le nombre servant à faire une bataille. C'est tout à fait ça, mais nous allons voir qu'il y a énormément d'implicites rendant la compréhension de ces nombres très laborieuse.
Lire les statistiques d'une carte
Comme de mon point de vue, il est probablement impossible de déduire
la relation entre ce fameux identifiant (dans notre exemple, le
fameux 1P23), je vais être très explicite, il nous donne quatre
informations sur la carte, de cette manière : PTDM où :
Pla puissance offensive de la carte, exprimée... en hexadécimal, de0àF, dans notre exemple, la valeur1;Tle type de la carte, pouvant prendre les valeursP,M,XoùA, dans notre exemple, la valeurPDla défense physique de la carte, exprimée elle aussi en hexadécimal, de0àF, dans notre exemple, la valeur2;Mla défense magique de la carte, exprimée elle aussi en hexadécimal, de0àF, dans notre exemple, la valeur3.
Je vous assure que le fait que les digits exprimés en hexadécimal
peuvent être, quand on commence à progresser dans l'aventure des
cartes, très déroutants. En effet, le jeu (et le manuel non plus
d'ailleurs) n'indiquant à aucun moment comment lire les
statistiques, alors que nous avions été habitué à voir au moins trois
chiffres, voir apparaitre des lettres peut provoquer beaucoup de
confusion ! D'autant plus que la statistiques AAAA est
parfaitement valide Donc même si comme moi, des années après vous
être heurté aux premiers contacts du Tetra Master, vous sortez
d'études d'informatique et que vous décidez, naïvement, de retenter
votre chance avec sa complexité effarante, quand bien même vous auriez
déjà été exposé au système de numération hexadécimal... fort à parier
que vous ne vous rendiez pas compte qu'il s'agit, en fait,
d'hexadécimal, le motifs de la statistique ne ressemblant absolument
pas à un nombre exprimé dans un système numérique connu.
Avant de nous étendre sur la signification concrète des valeurs hexadécimales (parce que oui, c'est beaucoup plus compliqué que ce que vous pouvez imaginer), voyons les différents types de cartes :
-
P(pour physical) est une carte qui utilisera sa puissance offensive pour attaquer la défense physique d'une autre carte. Par exemple dans la situation où7P23attaque2M12, nous aurons, dans les grandes lignes,7vs1; -
M(pour magical) est une carte qui utilisera sa puissance offensive pour attaquer, logiquement, la défense magique d'une autre carte. Par exemple, la situation où2M12attaque7P23, nous aurons, une fois de plus dans les grandes lignes2vs3; -
X(pour ... power (héhé) ou, selon les traductions, flexible) est une carte qui utilisera sa puissance offensive pour attaquer la plus faible des défenses d'une autre carte. Donc dans la situation où7X12attaque2M32, la carte ciblera, ici, la défense magique. Soit, une fois de plus dans les grandes lignes,7vs2; -
A(pour advanced ou assault) est une carte qui utilisera la plus haute de ses statistique (d'attaque ou de défense) pour attaquer la plus faible des autres point de statistiques (incluant la puissance offensive) d'une autre carte. Par exemple, dans la situation où2A8Fattaque1X2F, la carte utilisera sa défense magique pour cibler la puissance offensive de l'adversaire, soit, dans les grandes lignes,Fvs1.
Ce qui nous permet d'affirmer que FAFF est la meilleure statistique
envisageable pour une carte. Nous verrons qu'il est possible de faire
évoluer une carte, mais une difficulté à la fois ! Voyons d'abord
comment interpréter les chiffres en hexadécimal.
Interprétation des statistiques hexadécimales
Comme les statistiques exprimées en hexadécimal ne couvrent que 15
chiffres, il serait possible d'être relativement souvent en situation
d'égalité. Et bien ne vous en faites pas, le jeu nous réserve une
nouvelle surprise qui est, elle aussi, absolument absente du manuel du
jeu (ou dans l'explication, en jeu, des règles). En effet, ce serait
beaucoup trop simple que 9 veuille dire 9 ou que F veuille dire
15 !
Les statistiques exprimées en hexadécimal décrivent en fait des
intervalles. Ce qui implique que, par exemple que si EP12 attaque
2ME2, les deux E représentent des valeurs concrètes
potentiellement différentes. Il est évident que pour des raisons
d'ergonomie évidentes (je suis sarcastiques), il est impossible,
dans l'interface du jeu, de connaitre les valeurs concrètes de chaque
carte. Voici la liste des intervalles de valeurs possible pour
chaque niveau (la notation utilisée est celle des intervalles
ouverts
usuellement utilisée en mathématiques, où [a, b] décrit x >= a && x <= b) :
| Statistique | Intervalle | Statistique | Intervalle |
|---|---|---|---|
0 |
[0, 15] |
A |
[160, 175] |
1 |
[16, 31] |
B |
[176, 191] |
2 |
[32, 47] |
C |
[192, 207] |
3 |
[48, 63] |
D |
[208, 223] |
4 |
[64, 79] |
E |
[224, 239] |
5 |
[80, 95] |
F |
[240, 255] |
6 |
[96, 111] |
||
7 |
[112, 127] |
||
8 |
[128, 143] |
||
9 |
[144, 159] |
Comme il y a chaque fois 16 valeurs possibles par statistique, on
peut facilement décrire une formule systèmatique pour décrire
l'intervalle depuis un chiffre hexadécimal (dans la formule, nommé
n) :
let min = to_decimal(n) *. 16.0
let max = min +. 15.0
let range = (min, max)
Et oui, certains nombres devraient mettre la puce à l'oreille (par
exemple 32, 128 ou encore 255). En effet , n pourrait être
exprimer comme nF ce qui fait que chaque point de statistiques
(puissance offensive, défense physique et défense magique) est compris
entre 0 et 255. Donc, pour illustrer mon propos, la carte 4P0E
aura :
- une puissance offensive comprise entre
64et79; - une défense physique comprise entre
0et15; - une défense magique comprise entre
224et239.
Quand on le sait, c'est assez simple, cependant, comme il n'existe pas de moyen de connaitre explicitement la position dans l'intervalle, d'un point de vue, on se servira de la valeur minimale de l'intervalle pour éviter au maximum les faux-positifs. Maintenant que nous avons toutes les clés en mains pour lire correctement (mais... malheureusement partiellement) les statistiques d'une carte (qui est, selon moi, totalement exagérée et, je me répète, probablement impossible à déduire ne faisant que jouer) nous allons pouvoir observer le déroulement d'une bataille qui, évidemment, ajoute de la complexité et des aléas. Chic.
Déroulé de la bataille, toujours plus d'aléas
Maintenant que nous sommes capable de lire les statistiques d'une carte, couplé à la compréhension des flèches et des mécanismes de prises de cartes, nous devrions avoir assez d'éléments pour comprendre comment gagner toutes nos parties. Bien qu'il nous reste à décrire les combos, qui tiennent compte de la position des cartes sur le plateau et que nous détaillerons dans la rubrique suivante, on pourrait croire que nous avons suffisamment d'informations pour être capable de gagner des batailles locales. Cependant, les joueurs aguéris se rendront vite compte que les nombres affichés sur les cartes durant des batailles sont changeants et, encore pire, il arrivera que des scénarios qui semblent inéluctables ne se déroulent pas comme prévu !
Par exemple, imaginons une bataille entre les cartes 3P10
(attaquant) et 2M02 (défenseur). On oppose donc physiquement 3
(soit une puissance comprise entre 48 et 63) à 0 (soit une défense
comprise entre 0 et 15). Si notre interprétation des statistiques
est bonne, il n'existe aucun scénarios dans lesquels il est possible
d'imaginer que la carte attaquante perde. Et pourtant, ça arrivera. En
effet, il existe certains facteurs aléatoires permettant à une carte
plus faible de gagner une bataille. C'est pour l'application de ces
facteurs aléatoires que l'on verra, lors d'une bataille plusieurs
nombres s'afficher sur la carte.
Reprenons notre exemple 3P10, que l'on appellera X, attaquant
2M02, que l'on appellera Y. Comme nous l'avons évoqué, nous
opposons 3 à 0. Supposons ces différents faits :
- l'attaque de
Xsoit de50(soit une valeur comprise entre48et63) ; - la défense de
Ysoit de7(soit une valeur comprise entre0et15).
Ce sont ces premiers nombres qui seront affichés (et c'est donc la
seule manière de connaitre la position dans l'intervalle, même si nous
verrons plus tard que n'est pas fiable pour établir des stratégies sur
la durée car les cartes peuvent évoluer et que dans certaines
situations, par exemple en position de défense, il est difficile de
savoir quelle statistique est mise en avant, par exemple 1P22 contre
une carte de type X, comment savoir si le nombre affiché cible la
défense magique ou physique).
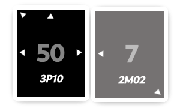
Ensuite, l'ordinateur définira un nombre aléatoire compris entre
0 et le précédent nombre affiché (donc pour X, entre 0 et 50
et pour Y, entre 0 et 7). On appellera ces nombre les
roulements Pour l'exemple, admettons ces différents faits :
Xa tiré pour roulement46;Ya tiré pour roulement1.
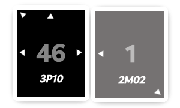
Les roulements sont respectivement soustraits aux valeurs concrètes de
l'intervalle. Comme chaque roulement est compris entre 0 et la
valeur concrète de l'intervalle, on ne pourra jamais avoir de nombres
négatifs.
Xaura50 - 46 = 4;Yaura7 - 1 = 6.
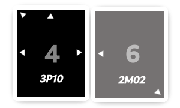
Et la carte ayant le résultat de la soustraction le plus élevé
l'emporte. Ici, contre toute attente, c'est la carte grise (semblant
largement moins puissante) qui l'emporte (parce que ... logiquement
4 < 6). Nous nous retrouvons donc Gros-Jean comme devant (désolé)
et notre carte noire est prise.
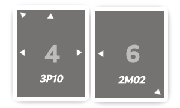
On se rend compte que les roulements influent beaucoup sur le
résultat de la bataille. En effet, au plus le roulement est élevé au
plus le risque de défaite est grand car le résultat est soustrait du
nombre concret de l'intervalle. Si par exemple le roulement de la
carte X avait été de 30, nous aurions eu 20 vs 6 et la carte
noire aurait gagné. Notre exemple a volontairement été pessimiste car
nous avons pris un très grand roulement. Cependant, en terme de
probabilité, la carte noire avait ~92% de chance de
gagner. Cependant, ça laisse tout de même ~8% de chance de défaite,
pouvant laisser un joueur ne connaissant pas les rouages complexes du
Tetra Master circonspect et frustré. De plus, cette règle repose sur
beaucoup d'éléments difficile à contrôler comme la position concrète
dans l'intervalle, couplé à de l'aléatoire, le tout dans un contexte
où le jeu est pauvrement expliqué et où la compréhension des
statistiques est laborieuse. Cet aléa ajoute, de mon point de vue,
énorme d'entropie dans la compréhension des règles, justifiant, au
moins un peu, les propos de Drew
Cosner,
cités en introduction de cet article, sur la teneur aléatoire du jeu.
En terme de feedback utilisateur, voir une carte afficher le nombre
40 et perdre contre une carte qui affiche le nombre 3 peut être
absolument incompréhensible (car oui, les nombres intermédiaire : le
roulement, et la soustraction ne sont absolument pas affichés).
Calcul des probabilités de victoire en duel
Le calcul de probabilité de victoire en cas de bataille est assez
facile à simuler. En voici une approximation qui, pour notre exemple
avec X = 50 et Y = 7 donnerait pour résultat ~92% :
let proba my_stat opponent_stat =
let a, b, need_reverse =
if my_stat > opponent_stat then (opponent_stat, my_stat, false)
else (my_stat, opponent_stat, true)
in
let x = 2.0 *. (1.0 +. b) and y = 1.0 +. a in
let result = 100.0 *. ((x -. y) /. x) in
if need_reverse then 100.0 -. result else result
Cependant, cette approche repose sur deux invariants qui ne sont généralement pas connu au moment de la partie, les deux positions concrètes dans l'intervalle. Une solution (acceptable) serait d'être très pessimiste concernant le calcul de ces probabilités en prenant la borne la plus basse de l'intervalle de ma carte et la borne la plus élevée de celle de l'opposant :
let pessimist_proba my_stat opponent_stat =
let my = to_decimal my_stat *. 16.0
and op = (to_decimal opponent_stat *. 16.0) +. 15.0 in
proba my op
Ce qui nous permet d'avoir une assez bonne idée des probabilités de victoire (un peu pessimiste mais, dans la vie, ne vaut-il pas mieux être prudent).
Le point amusant c'est qu'une fois que l'on connait :
- comment lire la représentation compressé des statistiques ;
- les facteurs aléatoires durant les batailles ;
- les points plus vaporeux (le nombre concret dans l'intervalle)
Les règles deviennent relativement peu complexes, et même si parfois, en tant que joueur, nous pouvons être frappés par l'aléatoire avec toutes ces informations, il est possible, une fois de plus, de mon point de vue, de prendre du plaisir, et de jouer plus sereinement, au Tetra Master. Bien que j'anticipe un peu la conclusion de cet article, le point de frustration essentiel réside dans la difficulté de découvrir les règles en lisant le manuel ou dans le jeu. Et je trouve qu'il est très étrange d'avoir explicitement pris la décision d'être aussi peu expansif sur comment lire les cartes et où l'aléatoire intervient. Sans plus attendre, passons aux combos qui, contre toute attente, eux, sont très prévisibles et compréhensibles sans lire les règles (yay) !
D'ailleurs, si pour une raison obscure, le code des probabilités vous intéresse, pour fluidifier l'écriture de cet article, j'ai écrit un tout petit programme qui me permet facilement d'avoir le pourcentage de réussite pessimiste d'une carte en attaquant une autre, vous pourrez trouver le code source sur ma page Github. Au moment où j'écris cet article, le programme ne fait pas grand chose mais il est possible que je passe, dans les jours/semaines/mois/années un peu de temps dessus pour, pourquoi pas, construire un véritable simulateur de Tetra Master, mais ne rêvons pas trop, le temps que m'a pris l'écriture de cet article risque de, potentiellement, me décourager d'aller plus loin.
Les combos
Il faut reconnaitre que le manuel est assez exhaustif sur le déroulé des combos, en effet, cette fois, pas d'aléatoire, pas de règles implicites, le manuel nous explique que : "Quand on gagne une bataille, toutes les cartes ciblées par les flèches de la carte fraichement gagnée sont aussi gagnées." que nous pourrions reformuler de cette manière : "En situation de bataille, toutes les cartes pointées par la carte perdante (donc venant d'être gagnée dans la bataille) sont aussi gagnées".

Il est important de souligner plusieurs points :
- même si la carte retournée pointe une autre carte en situation de bataille l'autre carte sera prise sans batailles ;
- les effets du combo ne se propagent pas récursivement (donc si une carte est prise parce qu'elle est ciblée par le perdant d'une bataille, les cartes qu'elle cible ne seront pas prises).
Les combos peuvent donc totalement inverser la tendance d'un match car il est possible de retourner jusqu'a 8 cartes en une seule bataille. Par exemple dans cette situation là :
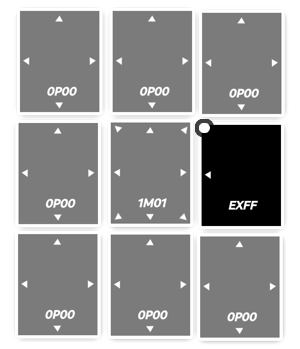
Cette situation (artificielle, je vous l'accorde) montre à quel point
une seule position de carte peut totalement changer l'issue d'une
partie. En effet, si la carte noire l'emporte (ce qui semblerait
normale étant donnée que dans pire des cas, soit 224 contre
15, elle possède une probabilité de 96.44% de chance de victoire),
elle retournera sa voisine, qui elle, retournera, sans aucune
bataille ses 7 voisines. Ce qui, dans la configuration actuelle du
plateau, implique que peu importe le coup suivant, le plus mauvais
scénario pour le joueur noir serait un match nul.
Couplée avec la mécanique des batailles multiples, les combos introduisent des micro-choix stratégiques amusants (et assez gratifiant en cas de victoire). Par exemple, si nous reprenons l'exemple présenté dans la section dédiée aux batailles multiples :

Dans cette situation, nous avons l'opportunité de choisir si nous
voulons attaquer la carte du dessus, qui a pour statistiques EXFF,
où de cibler la carte de droite, qui a pour statistiques 2M12. Pour
rappelle les probabilités de victoires (pessimistes) sont :
4P23vsEXFFde seulement12.70%;4P23vs2M12de75.38%.
Comme la carte de gauche pointe aussi la carte du haut, vaincre celle de gauche implique une prise, de facto, de la carte du haut. C'est un donc un coup largement plus pertinent à jouer ! Couplé avec les blocks dont nous avions parlé en détaillant la grille de jeu, mais aussi avec certaines cartes n'ayant pas de flèches (et bloquant donc la propagation des combos), il existe beaucoup de stratégies envisageables quand on joue au Tetra Master en essayant de se reposer au maximum sur les combos et à mon sens, c'est une excellente mécanique, bien documentée et dont il est facile de se rendre compte de son fonctionnement en jouant (même si la compréhension peut être un peu obfusquée par la difficulté de lecture de statistiques et les aléas imprévisibles du jeu).
Pré-conclusion sur les règles
À ce stade, même s'il reste quelques sujets à aborder, nous avons survolé l'ensemble des règles d'une partie et normalement, seuls les mauvais tirages de roulements devraient rendre les issues imprévisibles. Ce que l'on peut pré-conclure de l'exploration, en détail, du jeu, c'est qu'il semble assez amusant ! Cependant, l'absence d'un guide exhaustif (dans le jeu ou dans le manuel), couplé à des tirages aléatoires, rend le jeu très frustrant, comme en témoigne cette vidéo.
Par contre, rassurez-vous, le Tetra Master nous révèle encore quelques surprises, ayant une incidence directe sur le jeu, augmentant l'aléatoire, rendant donc l'inférence des règles encore plus laborieuse et pouvant, bien que partant d'une bonne intention (je l'espère), générer encore plus de frustration. Stay tuned.
Expérience et évolution des cartes
Nous en avions un peu parlé mais les cartes peuvent évoluer dans une limite définie (par carte) et nous allons voir que c'est, comme beaucoup de choses dans ce jeu, défini de manière assez aléatoire. En effet, au fil des combats, les cartes peuvent évoluer de deux manières différentes :
- leurs statistiques d'attaque et de défense (magique ou non) peuvent évoluer jusqu'à une certaine limite ;
- le type de la carte peut changer au fil de l'aventure.
Et ce qui est très amusant, c'est que ces deux évolutions peuvent arriver de manière parfaitement indépendantes. En d'autres termes, le type d'une carte peut évoluer sans que cette dernière ait atteint sa limite en attaque et défense. C'est pour ça que nous allons détailler les cas d'évolutions dans deux rubriques différentes et ensuite nous donnerons une liste des cartes avec les statistiques maximums qu'elles peuvent atteindre.
Evolution de l'attaque et des défenses
Une carte possède une statistique d'attaque et deux statistiques de
défense (la défense physique et la défense magique). Pour rappel, les
indices affichés sur la carte sont exprimé en hexadécimal et vont
de 0 F (15). Ses indices ne donnent pas la véritable valeur
associée à la carte mais un intervalle. Alors que des cartes de la
même effigies peuvent avoir un nombre de flèches différent et des
statistiques concrètes (la position dans l'intervalle) différentes,
lors de leur acquisitions, elles sont associées à une limite d'attaque
et de défense. Par exemple, la carte gobelin, possède, par défaut
la collection de statistiques suivante : 0P00, en d'autres mots, que
ses différents points d'attaque et de défense concrets peuvent aller
de 0 à 15. Par contre, on sait (par une obscure sorcellerie
parce que oui, évidemment que dans un jeu qui est aussi taiseux sur
son fonctionnement, être explicite sur les capacités maximum d'une
carte semble un peu surfait) qu'un gobelin peut avoir, au maximum
7 en attaque (toujour dans l'intervalle de 0), 9 de défense
physique et 4 de défense magique. Mais cependant, tant qu'une
carte n'a pas atteint ses limites, elle peut continuer à évoluer.
En effet, à chaque partie gagnée, chacune des cartes utilisée pendant
la partie se verra augmentée de 1 point une caractéristique
d'attaque ou de défense, choisie aléatoirement. Ce qui implique que,
à chaque combat gagné, chaque caractéristique aura une chance sur
trois d'être incrémentée. La seule manière de savoir quelle compétence
a été augmentée étant de faire entrer, dans une partie de carte
suivante, une des cartes de la partie précédente, dans une situation
de bataille pour voir son score effect a augmenté.
Un point amusant de cette décision aléatoire de la caractéristique à
incrémenter, c'est qu'elle ne tient absolument pas compte du fait
que la carte ait atteint sa limite. Donc si notre gobelin avait
déjà atteint 7 en attaque mais qu'il est à 6 en défense et 2 en
défense magique, mais que le hasard à décidé d'incrémenter les
statistiques d'attaques... le point est tout simplement perdu
... meh.
Une fois de plus, l'obfuscation de cette information (et son aléatoire) servent à compliquer la compréhension des règles du jeu ! Parce que oui, même si la notion d'expérience des cartes est, de mon point de vue, une très bonne idée qui motive à jouer au maximum, sans en informer le joueur, cette mécanique sert essentiellement à rendre la compréhension des statistiques (et des chiffres affichés sur la carte en situation de bataille) encore plus compliqué à inférer.
Evolution du type de cartes
En plus de pouvoir faire évoluer les compétences d'attaque et de
défense d'une carte, ces dernières peuvent aussi changer de
type. Toute carte de type P ou M peut évoluer en carte de type
X et toute carte de type X peut évoluer en carte de type A. Les
évolutions respectent donc cet organigrame, ce qui est très logique
car le type X est objectivement superieur au type M ou P, tout
en étant inferieur au type A :
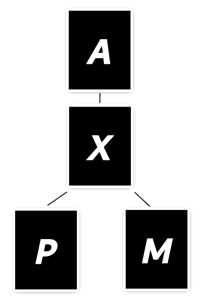
Au contraire des évolutions précédentes, conditionnées par la victoire
d'une partie, les cartes peuvent changer de type quand elles
remportent une bataille (peu importe qu'elles soient offensives ou
défensives). En effet, quand une carte gagne une bataille, si
c'est une carte P ou M, elle possède 1 chance sur 32 d'évoluer
en carte X et une carte X possède 1 chance sur 256 de passer
A.
Même si les chances d'évolution sont relativement faible, au
contraire des évolutions de points offensifs ou défensifs, les
changements de types sont largement plus facile à suivre (logique, ce
dernier est inscrit sur la carte). Quand nous nous intéresserons à la
dernière section (avant la conclusion) de cette article, le niveau
de collectionneur, nous verrons qu'il est nécessaire de faire monter
toutes les cartes niveau A, d'où l'importance de clarifier la
méthode pour réussir à faire qu'une carte atteigne ce niveau.
Liste des cartes
Comme les statistiques maximums des cartes ne sont évidemment pas données, voici une liste des 100 cartes accessibles dans le jeu, que j'ai trouvée ici, mais comme je suppose que la découverte des statistiques maximums, 20 ans plus tard, n'évoluera plus, je me permet de la reproduire ici, par soucis de vendorisation (je n'ai pas trouvé de traduction adéquate, désolé). Voici comment ce tableau se présente :
Nom, donne le nom, en Anglais, de la carte ;Type, donne son type original ;Atk, donne le nombre maximum de points (concrets) d'attaque possible ;Def, donne le nombre maximum de points (concrets) de défense possible ;Atk, donne le nombre maximum de points (concrets) de défense magique possible ;MStatsdonne la statistique maximum affichable sur la carte. (Elles seront toutes de typeAcar toutes les cartes peuvent atteindre ce type).
la liste de cartes
| Id | Nom | Type | Atk | Def | MDef | MStats |
|---|---|---|---|---|---|---|
001 |
Gobelin | P |
7 |
9 |
4 |
0A00 |
002 |
Fang | P |
9 |
10 |
4 |
0A00 |
003 |
Skeleton | P |
11 |
12 |
10 |
0A00 |
004 |
Flan | M |
13 |
6 |
19 |
0A01 |
005 |
Zaghnol | P |
15 |
13 |
13 |
0A00 |
006 |
Lizard Man | P |
17 |
15 |
8 |
1A00 |
007 |
Zombie | P |
19 |
19 |
11 |
1A10 |
008 |
Bomb | M |
21 |
12 |
21 |
1A01 |
009 |
Ironite | P |
23 |
23 |
13 |
1A10 |
010 |
Sahagin | P |
25 |
18 |
4 |
1A10 |
011 |
Yeti | M |
27 |
6 |
26 |
1A01 |
012 |
Mimic | M |
29 |
20 |
27 |
1A11 |
013 |
Wyerd | M |
31 |
9 |
33 |
1A02 |
014 |
Mandragora | M |
33 |
15 |
39 |
2A02 |
015 |
Crawler | P |
35 |
36 |
8 |
2A20 |
016 |
Sand Scorpion | P |
37 |
37 |
17 |
2A21 |
017 |
Nymph | M |
39 |
12 |
38 |
2A02 |
018 |
Sand Golem | P |
41 |
38 |
16 |
2A21 |
019 |
Zuu | P |
43 |
11 |
34 |
2A02 |
020 |
Dragonfly | P |
45 |
40 |
19 |
2A21 |
021 |
Carrion Worm | M |
47 |
29 |
25 |
2A11 |
022 |
Cerberus | P |
49 |
45 |
4 |
3A20 |
023 |
Antlion | P |
51 |
48 |
27 |
3A31 |
024 |
Cactuar | P |
53 |
195 |
4 |
3AC0 |
025 |
Gimme Cat | M |
55 |
33 |
29 |
3A21 |
026 |
Ragtimer | M |
57 |
34 |
30 |
3A21 |
027 |
Hedgehog Pie | M |
59 |
22 |
40 |
3A12 |
028 |
Ralvuimahgo | P |
61 |
68 |
12 |
3A40 |
029 |
Ochu | P |
63 |
37 |
18 |
3A21 |
030 |
Troll | P |
65 |
62 |
34 |
4A32 |
031 |
Blazer Beetle | P |
67 |
91 |
18 |
4A51 |
032 |
Abomination | P |
69 |
59 |
58 |
4A33 |
033 |
Zemzelett | M |
71 |
32 |
96 |
4A26 |
034 |
Stroper | P |
73 |
64 |
8 |
4A40 |
035 |
Tantarian | M |
75 |
43 |
39 |
4A22 |
036 |
Grand Dragon | P |
77 |
65 |
71 |
4A44 |
037 |
Feather Circle | M |
79 |
45 |
41 |
4A22 |
038 |
Hecteyes | M |
81 |
10 |
70 |
5A04 |
039 |
Ogre | P |
83 |
80 |
29 |
5A51 |
040 |
Armstrong | M |
85 |
36 |
75 |
5A24 |
041 |
Ash | M |
87 |
50 |
50 |
5A33 |
042 |
Wraith | M |
89 |
80 |
17 |
5A51 |
043 |
Gargoyle | M |
91 |
51 |
47 |
5A32 |
044 |
Vepal | M |
93 |
52 |
48 |
5A33 |
045 |
Grimlock | M |
84 |
37 |
54 |
5A23 |
046 |
Tonberry | P |
41 |
54 |
50 |
2A33 |
047 |
Veteran | M |
90 |
30 |
145 |
5A19 |
048 |
Garuda | M |
98 |
72 |
29 |
6A41 |
049 |
Malboro | M |
86 |
57 |
99 |
5A36 |
050 |
Mover | M |
102 |
250 |
8 |
6AF0 |
051 |
Abadon | M |
125 |
105 |
45 |
7A62 |
052 |
Behemoth | P |
189 |
71 |
106 |
BA46 |
053 |
Iron Man | P |
197 |
110 |
12 |
CA60 |
054 |
Nova Dragon | P |
236 |
125 |
194 |
EA7C |
055 |
Ozma | P |
221 |
6 |
199 |
DA0C |
056 |
Hades | M |
250 |
200 |
20 |
FAC1 |
057 |
Holy | M |
134 |
40 |
63 |
8A23 |
058 |
Meteor | M |
190 |
162 |
2 |
BAA0 |
059 |
Flare | M |
208 |
17 |
17 |
DA11 |
060 |
Shiva | M |
83 |
6 |
95 |
5A05 |
061 |
Ifrit | M |
100 |
150 |
17 |
6A91 |
062 |
Ramuh | M |
74 |
29 |
103 |
4A16 |
063 |
Atomos | M |
66 |
100 |
100 |
4A66 |
064 |
Odin | M |
205 |
136 |
72 |
CA84 |
065 |
Leviathan | M |
183 |
100 |
22 |
BA61 |
066 |
Bahamut | M |
200 |
145 |
83 |
CA95 |
067 |
Ark | M |
226 |
96 |
90 |
EA65 |
068 |
Fenrir | M |
139 |
36 |
22 |
8A21 |
069 |
Madeen | M |
162 |
22 |
100 |
AA16 |
070 |
Alexander | M |
225 |
183 |
86 |
EAB5 |
071 |
Excalibur II | P |
255 |
180 |
6 |
FAB0 |
072 |
Ultima Weapon | P |
248 |
24 |
102 |
FA16 |
073 |
Masamune | P |
202 |
180 |
56 |
CAB3 |
074 |
Elixir | M |
100 |
100 |
100 |
6A66 |
075 |
Dark Matter | M |
199 |
56 |
195 |
CA3C |
076 |
Ribbon | M |
12 |
200 |
255 |
0ACF |
077 |
Tiger Racket | P |
12 |
5 |
19 |
0A01 |
078 |
Save the Queen | P |
112 |
60 |
10 |
7A30 |
079 |
Genji | P |
10 |
105 |
175 |
0A6A |
080 |
Mythril Sword | P |
32 |
4 |
6 |
2A00 |
081 |
Blue Narciss | P |
143 |
144 |
20 |
8A91 |
082 |
Hilda Garde 3 | P |
98 |
62 |
16 |
6A31 |
083 |
Invincible | M |
185 |
145 |
201 |
BA9C |
084 |
Cargo Ship | P |
45 |
100 |
10 |
2A60 |
085 |
Hilda Garde 1 | P |
99 |
75 |
2 |
6A40 |
086 |
Red Rose | P |
143 |
20 |
144 |
8A19 |
087 |
Theater Ship | P |
33 |
106 |
19 |
2A61 |
088 |
Viltgance | P |
228 |
145 |
32 |
EA92 |
089 |
Chocobo | P |
3 |
5 |
12 |
0A00 |
090 |
Fat Chocobo | P |
25 |
30 |
30 |
1A11 |
091 |
Mog | M |
3 |
5 |
12 |
0A00 |
092 |
Frog | P |
2 |
2 |
2 |
0A00 |
093 |
Oglop | P |
40 |
33 |
6 |
2A20 |
094 |
Alexandria | P |
4 |
178 |
100 |
0AB6 |
095 |
Lindblum | P |
6 |
100 |
178 |
0A6B |
096 |
Two Moons | M |
113 |
88 |
88 |
7A55 |
097 |
Gargant | P |
46 |
17 |
56 |
2A13 |
098 |
Namingway | M |
127 |
127 |
127 |
7A77 |
099 |
Boco | P |
128 |
127 |
127 |
8A77 |
100 |
Airship | P |
129 |
127 |
127 |
8A77 |
Maintenant, que vous savez comment faire monter les statistiques d'une carte et changer son type, nous allons pouvoir nous intéresser aux dernières sources d'incompréhension de ce jeu ... le niveau de collectionneur.
Le niveau de collectionneur
Les règles du jeu et la logique d'évolution des cartes n'ont plus de secrets pour nous, nous pouvons nous intéresser à la dernière énigme du jeu, le fameux niveau de collectionneur. Quand on se rend dans le menu des cartes (depuis le menu principal), on peut observer l'ensemble de sa collection de cartes, et lire plusieurs statistiques.
- le nombre de parties gagnées ;
- le nombre de parties perdues ;
- le nombre de matchs nuls ;
- Le
niveau, exprimé enp.
Les trois premières informations ne devraient (à priori) pas nécéssiter de clarifications. Le jeu garde en mémoire une trace des parties effectuées et fourni, par le biais de ce menu, une synthèse. Par contre, ce qui attire notre attention est le niveau. En effet, en observant l'évolution de ce niveau au fil des parties, comme beaucoup d'éléments du Tetra Master, il est très difficile de comprendre la manière dont ce compteur évolue (une fois n'est pas coutume, on est face à une règle assez capilotractée).
Encore plus amusant, on peut rapidement se rendre compte que les trois éléments de synthèse (victoires, défaites et nuls) n'influent pas réellement sur ce score. En effet, il existe plusieurs situations dans lesquelles l'issue d'une partie ne changeront pas le niveau. Et oui, comme souvent dans ce jeu, pourquoi se contenter de quelque chose de simple et de déductible quand on peut choisir une métrique éclatée au sol ? Pour faire simple, le niveau est déterminé par les cartes que l'on possède, selon une mécanique très spécifique que nous allons, sans plus tarder détailler.
Les différents niveaux
Avant de décrire comment calculer les points en fonction des cartes possédées, voici la liste des différents niveaux qu'il est possible d'atteindre dans le jeu. Pour rappel, votre niveau aux cartes n'aura aucune incidence sur le déroulé du jeu.
| Points minimum | Niveau de collectionneur |
|---|---|
>= 0 |
Beginner |
>= 300 |
Novice |
>= 400 |
Player |
>= 500 |
Senior (developper) |
>= 600 |
Fan |
>= 700 |
Leader |
>= 800 |
Coach |
>= 900 |
Advisor |
>= 1000 |
Director |
>= 1100 |
Dealer |
>= 1200 |
Trader |
>= 1250 |
Commander |
>= 1300 |
Doctor |
>= 1320 |
Professor |
>= 1330 |
Veteran |
>= 1340 |
Freak |
>= 1350 |
Champion |
>= 1360 |
Analyst |
>= 1370 |
General |
>= 1380 |
Expert |
>= 1390 |
Shark |
>= 1400 |
Specialist |
>= 1450 |
Elder |
>= 1475 |
Dominator |
>= 1500 |
Maestro |
>= 1550 |
King |
>= 1600 |
Wizard |
>= 1650 |
Authority |
>= 1680 |
Emperor |
>= 1690 |
Pro |
= 1698 |
Master |
Amusant d'avoir autant d'étapes de progression pour une logique de gain de points aussi difficile à déduire, n'est-il pas ? Une fois de plus, on pourra râler de l'excès d'implicites dans ce jeu, où chaque décision semble avoir été prise pour perdre le joueur. Comme nous allons le voir dans les sections qui suivent, le calcul des points est loin d'être trivial !
Sur la distinction des cartes
Avant de détailler la corrélation entre les cartes possédées et les points qu'elles rapportent, il est important de donner quelques clarifications terminologiques. Voici les éléments qui caractérisent une carte pour le calcul des points :
- sa figure, par exemple
GobelinouFat Chocobo; - son motif de flèches ;
- son type (
XouA).
Les cartes de types P ou M n'apportent pas de bonus de points et
les statistiques des cartes (donc leur évolution), n'influent pas dans
le calcul des points.
Donc quand on parle d'une carte unique, on parle d'une carte avec une figure spécifique que l'on ne possède qu'une seule fois. Quand on parle d'une carte additionnelle on parle d'une carte avec une figure que l'on possède plusieurs fois.
Les points attribués par cartes
Les points sont calculés en fonction des cartes que l'on possède et de la manière dont sont arrangés leurs flèches (outch). De manière schématique, on pourrait définir que les axes permettant se gagner des points sont :
-
la diversité des cartes que l'on possède. Dans l'absolu, c'est assez simple, on ne peut posséder que
100cartes simultanément et il n'existe que100figures de cartes (par exemple Gobelin). Il faut donc, pour maximiser ses points, n'avoir que des figures différentes ; -
la diversité des motifs de flèches des cartes que l'on possède. En vue de maximiser ses points, chaque carte devrait avoir un motif de flèche unique (non non, ce n'est pas une blague) ;
-
la puissance des cartes que l'on possède. Les cartes
XetAdonnent un bonus de point, donc pour maximiser ses points, toutes les cartes devraient être niveauA(qui rapporte le plus de points).
Voici de quelle manière une carte peut faire gagner des points, les
caractéristiques sont cumulables (sauf, évidemment, dans le cas du
type de la carte, parce que ... logiquement, une carte ne peut pas
être simultanément X ou A) :
| Caractéristique | Récompense |
|---|---|
| Carte unique ? | + 10 points |
| Motif de flèches unique ? | + 5 points |
Si c'est une carte X ? |
+ 1 point |
Si c'est une carte A ? |
+ 2 point |
Donc pour atteindre le niveau maximum de points possible, il faut
n'avoir que des cartes uniques (figures différentes et motifs de
flèches différents) et qu'elles soient toutes au niveau A. On peut
donc déduire le nombre de points nécessaire pour atteindre le niveau
maximum : 1700, parce qu'il y a 100 cartes et que le score
maximum que peut atteindre une carte (unique sur la figure et le
motif et de type A) est 17.
Note sur les permutations de motifs
On sait qu'une carte peut avoir entre 0 et 8 flèches. En
d'autres termes, on pourrait dire que pour chacun des 8 espaces
libres (slots) il peut y avoir une flèche ou pas. Ce qui correspond
à 256 permutations possibles. On peut facilement s'en convaincre en
décrivant le chaque slot par un booléen, 0 où '1', on obtient,
dans le cas où tous les slots sont occupés une succession de huit
1, 11111111, soit la représentation binaire de 256.
On pourrait même décrire, par nombre de flèches, le nombre de combinaisons possibles avec cette formule :
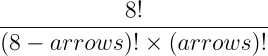
Ce qui nous donne comme liste des combinaisons possibles pour chaque
nombre de flèches, ce qui nous indique que nous ne sommes pas obligé
d'avoir des motifs faibles pour attendre le niveau le plus élevé. En
effet, il y a 163 combinaisons incluant au minimum 4 flèches :
| Flèches | Permutations |
|---|---|
| 0 | 1 |
| 1 | 8 |
| 2 | 28 |
| 3 | 56 |
| 4 | 70 |
| 5 | 56 |
| 6 | 28 |
| 7 | 8 |
| 8 | 1 |
| 256 permutations |
Alors que pour atteindre le maximum, vous devez avoir toutes les cartes et
elles doivent tout être au niveau A, vous ne devez vous embarasser que de
~39% (100 sur 256) des motifs de flèches différents. Chic.
La cerise sur le gateau
Si vous avez été attentifs, vous auriez dû remarquer quelque
chose. Alors que nous avions dit que chaque carte pouvait rapporter
au maximum 17 points et qu'il y en avait 100, donc, qu'il était
possible de collecter 1700 points, le tableau des niveaux, lui,
s'arrête à 1698. Alors que se passe-t-il si l'on atteint 1700 ? On
pourrait s'attendre à une surprise d'envergure, par exemple, un objet
rare, ou encore les félicitations d'un PNJs. Et bien la réponse nous
est données par ik141 (et reportée par le sombre document, je
n'ai malheureusement pas pu retrouver le message original) qui lui, a
fait l'effort d'obtenir le niveau maximum envisageable dans le
Tetra Master :
So what happens at
1700, you ask? Well, under your collector pts. whereMasterwas written it now says, superimposed over everything, 'Would you like to discard?'. So, after a hundred hours of playing this game I am rewarded with a F***ING GLITCH!!!"
Je suis emmerveillé de terminer la longue description des règles du Tetra Master sur cette note de bonne humeur. Vous ne rêvez pas, le guide ou à été consigné ce témoignage de frustation est approximativement contemporain à la sortie du jeu. L'exploit de ik141 est donc très impressionnant car :
- il ne bénéficiait pas du guide que j'ai utilisé pour comprendre les règles ;
- l'état de l'art de l'émulation n'était pas encore au niveau où il est aujourd'hui. On peut donc supposer (mais ce n'est peut-être que de la spéculation) que ce prodige des cartes à tenté de terminer le jeu, incluant la quête du Tetra Master ... à l'ancienne.
Et Squaresoft (par l'entremise des développeurs et concepteurs du jeu de cartes) est aussi extraordinaire d'avoir parsemé le chemin de la compréhension des règles d'embûches pour, au final, offrir un glitch en fin d'épopée. C'est sur le témoignage de cette incroyable chute que nous en avons terminé avec les règles du Tetra Master et nous pouvons, sans plus tarder, passer à la conclusion de ce très long article.
Pour conclure, enfin
Une page se tourne. J'ai découvert FFIX il y a plus de 20 ans, et à chaque tentative, le Tetra Master m'a toujours laissé un goût d'amertume dans en travers de la gorge. Après deux tentatives (une en 2012 par émulation et une en 2020, sur Nintendo Switch) de comprendre les règles du jeu dans le jeu, j'ai abandonné pour m'aider d'internet. C'était une investigation très amusante qui me fait m'interroger sur la réelle qualité du jeu. Me plonger dans les règles du Tetra Master altère la conclusion que je pensais avoir en commençant à rédiger cet article. Ayant été un très grand amateur du neuvième opus de cette saga qui m'a tant marqué, mon impuissance face au Tetra Master a généré de le frustration et de l'aigreur. Quand j'ai commencé à me documenter, j'étais furieux de ce que je lisais et j'étais persuadé que ma conclusion serait assassine. Cependant, probablement parce que j'ai développé un genre de syndrome de Stockholm, depuis que je connais les règles du jeu, j'ai développé une sympathie macabre pour le Tetra Master. Je suis très content d'avoir appris, enfin, à y jouer.
Pour conclure cet article (qui m'aura pris plus de 15 jours de rédaction, mais j'ai fais beaucoup de pauses), je vais essayer de donner un avis nuancé sur le jeu.
Qu'en tirer
Que ce soit sur Youtube ou sur
Reddit, les avis sont mitigés. Certains
détestent le Tetra Master, d'autres l'adorent. Cependant, sans être de
mauvaise foi, l'énorme majorité des gens qui donnent leur avis
semblent être tous d'accord, le jeu est trop compliqué et ses règles
sont impossible à déduire. Pour ma part, maintenant que je pense
avoir compris toutes les règles du jeu, j'ai beaucoup de mal à le
considérer comme un mauvais jeu. Il fourmille de collections de bonnes
idées. Par exemple, le fait de calculer le niveau du
collectionneur sur base des cartes et non sur le rapport
victoire/défaite permet de moduler son score au plus on avance dans
le jeu, ne rendant presque aucune défaite trop pénalisante.
Un autre retour assez populaire sur le jeu, comme en témoigne ce thread Reddit est la présence d'aléatoire. Aux premiers abords, j'étais assez d'accord avec le fait de conspuer l'aléatoire. Cependant, avec un peu de recul, j'en arrive à la conclusion que l'aléatoire est présent dans une grande partie de jeux de cartes populaires. Par exemple quand le jeu introduit une pioche de cartes ou encore par le fait que l'on ne connaisse pas la main de l'adversaire et certains jeux ne reposent que sur de l'aléatoire (la très populaire bataille par exemple).
Pour ma part, ce que je reproche réellement au jeu est l'impossibilité de déduire ses règles et le trop peu de retour utilisateurs. J'ai l'intime conviction que si le jeu était plus explicite, in game ou dans son manuel concernant ses règles (et ses différentes mécaniques) et que si les statistiques réelles des cartes étaient consultable depuis un menu (et expliquée, évidemment), la réception du jeu n'aurais pas été si mauvaise. D'ailleurs, je suis assez curieux de savoir comment la présentation (et la réception) de la proposion du Tetra Master s'est déroulée chez Squaresoft.
Pour conclure, je pense que certaines règles pourraient être simplifiée, et que le jeu devrait disséminer plus d'informations et d'explications. Par contre, et contre toutes attentes, quand on connait les règles, le jeu est largement plus ludique que ce que l'on pourrait imaginer. Et si vous avez eu le courrage d'arriver jusqu'ici, dans cet article, je serais curieux d'avoir votre retour sur l'expérience du jeu une fois que l'on connait les règles !
La suite
Il est très amusant de développer un intérêt pour un jeu en décrivant ses règles parce qu'on les trouvait incompréhensible. Il est donc possible que je ne m'arrête pas là. En effet, la rédaction de cet article m'a donnée l'envie, si le temps me le permet, d'en proposer une implémentation libre (même s'il est probable que ce projet n'aboutisse jamais, faute de temps et de motivation).
Remerciements
Le premier remerciement que je souhaite adresser est pour Trifthen, je n'ai aucune idée de qui il est, mais sans son guide qui est devenu une référence sur internet quand on essaie de comprendre les règles du Tetra Master, je n'aurais jamais pu écrire ma version (qui est plus naïve, je vous l'accorde). La précision et l'exhaustivité de son travail m'ont parfois poussé à abandonner la rédaction de l'article, me disant que je n'avais rien à apporté à son document. Mais bon, mon site personnel étant dans un état léthargique, un peu de contenu ne fais pas de mal !
Ensuite, pour croiser les informations du guide de Trifthen, je voudrais spécialement remercier Antoine pour m'avoir donné accès à des ressources que je ne peux malheureusement pas partager dans cet article ainsi que tous les mainteneurs de ePSXe me permettant de naviguer dans des informations internes au jeu.
L'envie de me réintéresser aux Jeux-vidéo (et essentiellement au J-RPG) a été grandement stimulé par Bastien m'ayant fait le plaisir, en Aout, de m'offrir l'excellent livre A Guide to Japanese Role-Playing Games dont la lecture des premières pages m'a directement (et instantanément) donné envie de retenter de fabriquer un RPG (en me laissant plus de temps que pour la construction de Almost Heroic).
Je remercie aussi très chaleureusement Lorie qui a subi mon étrange monomanie, pendant tout une soirée, où j'ai témoigné d'un sentiment mélangeant l'émerveillement et la terreur face à la cathétrale de complexité que semblaient être les règles du Tetra Master. Son écoute et ses questions ont permis de clarifier certains points (et certains choix terminologiques) et aussi pour sa relecture potentielle, améliorant ma désastreuse orthographe et mes tournures de phrases maladroites (qu'il est utile et plaisant d'avoir dans son entourage des gens ayant une acquaintance naturelle pour l'expression écrite et l'amour des belles phrases).
Après la publication de cet article, j'ai reçu une collection des revues et de retours, incluant Hakim, Matthieu, l'inénarrable Fenn ainsi que de Maël, merci à vous !
Pour terminer, je souhaite remercier les différentes personnes ayant encensé ou critiqué le jeu sur les différents médiums qu'offre l'Internet mondial ainsi que les lecteurs potentiels ayant réussi à digérer ce très long article, sur un sujet si dépassé !
L'ultime mot de la fin
Plus de vingt ans plus tard, une page se tourne. Il est difficile de me considérer comme un adulte sans avoir compris les règles du Tetra Master. C'est chose faite ! Je peux maintenenant me concentrer sur des projets moins intéressants et moins formatteurs ! Blagues à part, j'ai eu beaucoup d'amusement à faire ce travail d'archéologie, de rédaction (et un peu d'implémentation). C'était très rigolo et je tâcherai d'être plus régulier dans ma rédaction, en, pourquoi pas, continuant dans la description de mécaniques de jeu ! Encore merci pour votre lecture et très bonne canicule.